Результат вспучивания и раздутия: Результат вспучивания и раздутия | Поле Чудес ответы – Поле чудес : Результат вспучивания и раздутия : Смотреть ответ

Раздутие — Википедия

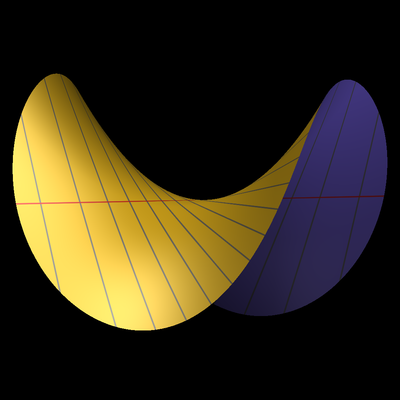Окрестность точки в вещественной плоскости после раздутия. Красным цветом показана исключительная кривая. Синие прямые до раздутия проходили через раздутую точку. Каждая точка исключительной красной кривой соответствует единственной синей прямой. При стремлении к бесконечности вдоль двух направлений исключительной кривой синие прямые загибаются под противоположными углами, и видно, что на бесконечности они склеятся с перекруткой, образуя лист Мёбиуса.

Разду́тие^[1][2][3] (называемое Тюриным сигма-процессом^[4], а Маниным моноидальным преобразованием^[5]) — операция в алгебраической геометрии. В простейшем случае оно, грубо говоря, оно состоит в замене точки на множество всех прямых, проходящих через неё.

Пусть P2{\displaystyle \mathrm {P} ^{2}} — проективная плоскость, а P2ˇ{\displaystyle {\check {\mathrm {P} ^{2}}}} — двойственная проективная плоскость, точки которой соответствуют прямым исходной плоскости. Точки декартова произведения P2×P2ˇ{\displaystyle \mathrm {P} ^{2}\times {\check {\mathrm {P} ^{2}}}} — это пары (x,ℓ){\displaystyle (x,\ell )}, где x{\displaystyle x} — точка плоскости, a ℓ{\displaystyle \ell } — прямая в той же плоскости. Условие x∈ℓ{\displaystyle x\in \ell } того, что точка лежит на прямой, в координатных терминах описывается как зануление линейной формы на векторе, так что множество {(x,ℓ):x∈ℓ}⊂P2×P2ˇ{\displaystyle \left\{(x,\ell )\colon x\in \ell \right\}\subset \mathrm {P} ^{2}\times {\check {\mathrm {P} ^{2}}}} является алгебраическим многообразием. Более того, поскольку произведение проективных пространств вкладывается в проективное пространство достаточно большой размерности при помощи вложения Сегре, оно является также и проективным многообразием. Оно называется многообразием инцидентности. Обозначим его за I{\displaystyle I}. Зафиксируем точку x0∈P2{\displaystyle x_{0}\in \mathrm {P} ^{2}}, рассмотрим многообразие Fx0={(x,ℓ):x0∈ℓ}{\displaystyle F_{x_{0}}=\{(x,\ell )\colon x_{0}\in \ell \}} и его пересечение Fx0∩I{\displaystyle F_{x_{0}}\cap I} с многообразием инцидентности. Рассмотрим ограничение проекции P2×P2ˇ→P2{\displaystyle \mathrm {P} ^{2}\times {\check {\mathrm {P} ^{2}}}\to \mathrm {P} ^{2}} на это пересечение. Если точка x∈P2{\displaystyle x\in \mathrm {P} ^{2}} отлична от точки x0{\displaystyle x_{0}}, то слой проекции над ней состоит из единственной точки (x,ℓ){\displaystyle (x,\ell )}, где ℓ{\displaystyle \ell } — прямая, проходящая через точки x{\displaystyle x} и x0{\displaystyle x_{0}}. С другой стороны, слой над самой точкой x0{\displaystyle x_{0}} состоит из всех прямых, которые через неё проходят. Многообразие Fx0∩I{\displaystyle F_{x_{0}}\cap I} обозначается Blx0(P2){\displaystyle \mathrm {Bl} _{x_{0}}(\mathrm {P} ^{2})} и называется раздутием плоскости P2{\displaystyle \mathrm {P} ^{2}} в точке x0{\displaystyle x_{0}}. Таким образом, это раздутие отличается от плоскости тем, что одна из точек в нём заменена на прямую. В случае, когда проективная плоскость определена над полем комплексных чисел, проективная прямая является сферой Римана, что и объясняет название. Вклеивающаяся прямая называется исключительной кривой и традиционно обозначается Ex0{\displaystyle E_{x_{0}}}. Она отличается от обычных прямых тем свойством, что не допускает аналитических деформаций.

Пусть C{\displaystyle C} — алгебраическая кривая, проходящая через точку x0{\displaystyle x_{0}}. Теоретико-множественный прообраз C{\displaystyle C} относительно проекции Blx0→P2{\displaystyle \mathrm {Bl} _{x_{0}}\to \mathrm {P} ^{2}} содержит исключительную кривую Ex0{\displaystyle E_{x_{0}}} и называется полным прообразом. Тем самым полный прообраз не является неприводимым, даже если изначальная кривая была неприводимой. Однако если в качестве прообраза точки x0{\displaystyle x_{0}} брать только те пары (x0,ℓ){\displaystyle (x_{0},\ell )}, где ℓ{\displaystyle \ell } — касательная к одной из ветвей кривой в этой точке, то прообраз неприводимой кривой будет неприводим. Такой прообраз называется собственным прообразом. Если x0{\displaystyle x_{0}} — гладкая точка кривой, то собственный прообраз будет изоморфен самой кривой. Если же кривая имела особенность в этой точке, то собственный прообраз будет отличаться. Например, собственный прообраз декартовой кубики при раздутии в начале координат есть гладкая рациональная кривая.

Секции Шуховской башни — подмножества вещественных квадрик. Балки, из которых она составлена, являются кривыми, сдувающимися при проекции на плоскость из их перекрестья.

Заметим, что вышеописанная конструкция могла быть проделана в пределах аффинной карты. Значит, можно говорить о раздутиях любой алгебраической поверхности (или, более общо, комплексной поверхности). Топологически раздутие устроено следующим образом: у точки x0{\displaystyle x_{0}} вырезается маленькая окрестность, выглядящая как четырёхмерный шар, и к его границе — трёхмерной сфере — приклеивается двумерная сфера при помощи отображения Хопфа. Раздутие вещественной поверхности состоит в вырезании небольшого диска и приклеивании к его границе, окружности, ленты Мёбиуса.

Заметим, что раздутие не является настоящим отображением, а лишь рациональным отображением: раздутие не определено корректно в раздуваемой точке. При этом обратная операция, называемая сдутием или стягиванием, хорошо определена. Российский геометр А. И. Бондал формулировал это следующим образом: «по определению, раздутие — это операция, противоположная сдутию».

Не любую рациональную кривую на поверхности можно сдуть. Например, на плоскости никакая кривая не допускает сдутия, поскольку небольшое изменение коэффициентов её уравнения даёт деформацию кривой, которых у исключительных кривых раздутий быть не может. Критерий (англ.)русск. сдуваемости кривой на алгебраической поверхности был открыт Г. Кастельнуово и является одним из классических достижений итальянской школы.

Например, если раздуть на проективной плоскости две точки, то собственный прообраз проходящей через них прямой будет сдуваем. При его сдутии получается квадрика. Пучки прямых, проходящих через эти две точки, при таком преобразовании перейдут в два семейства прямых на квадрике. Обратное преобразование можно наглядно описать следующим образом. Рассмотрим квадрику Q{\displaystyle Q} в трёхмерном проективном пространстве и точку x{\displaystyle x} на ней, а также какую-нибудь плоскость Π{\displaystyle \Pi }, не проходящую через x{\displaystyle x}. Сопоставим точке y∈Q{\displaystyle y\in Q} точку пересечения прямой xy{\displaystyle xy} с плоскостью Π{\displaystyle \Pi }. Чтобы эта операция была корректно определена в точке x{\displaystyle x}, нужно сначала раздуть в ней квадрику. Проекция Blx(Q)→Π{\displaystyle \mathrm {Bl} _{x}(Q)\to \Pi } хорошо определена и взаимно-однозначна вне двух прямых на квадрике, проходящих через центр проекции. Таким образом, проекция сдувает эти прямые в две точки.

Критерий Кастельнуово полезен при классификации алгебраических поверхностей (англ.)русск.: после всех возможных сдутий получается так называемая минимальная модель алгебраической поверхности, такие поверхности расклассифицировать уже нетрудно. Также сдутия полезны в других вопросах алгебраической геометрии поверхностей: например, двумерная группа Кремоны (англ.)русск. (группа рациональных преобразований проективной плоскости) порождается композициями раздутий и сдутий.

На алгебраической поверхности можно раздуть лишь конечное число точек. Тем не менее, можно имитировать раздутие плоскости во

всех точках, рассмотрев пределы решёток Нерона — Севери по всевозможным раздутиям. Получающийся объект называется пространством Пикара — Манина. Это бесконечномерное пространство Минковского, на котором действует группа Кремоны. Французские геометры С. Канта и С. Лами доказали, рассмотрев это действие, что группа Кремоны не является простой.^[6]

Наиболее плодотворное описание раздутий в больших размерностях даётся в теории схем. Например, если X{\displaystyle X} — проективная схема, a I{\displaystyle {\mathcal {I}}} — когерентный пучок идеалов на ней, то раздутием схемы в идеале называется схема BlI(X){\displaystyle \mathrm {Bl} _{\mathcal {I}}(X)} вместе с отображением схем π:BlI(X)→X{\displaystyle \pi \colon \mathrm {Bl} _{\mathcal {I}}(X)\to X} таким, что, во-первых, пучок π−1(I)⋅OBlI(X){\displaystyle \pi ^{-1}({\mathcal {I}})\cdot {\mathcal {O}}_{\mathrm {Bl} _{\mathcal {I}}(X)}} обратим, а во-вторых, любой морфизм f:Y→X{\displaystyle f\colon Y\to X} такой, что пучок f−1(I)⋅OY{\displaystyle f^{-1}({\mathcal {I}})\cdot {\mathcal {O}}_{Y}} обратим, единственным образом пропускается через морфизм π{\displaystyle \pi }. Это универсальное свойство определяет раздутие единственным образом. Явно раздутие определяет конструкция Proj как Proj⨁i=0+∞Ii{\displaystyle \mathrm {Proj} \bigoplus _{i=0}^{+\infty }{\mathcal {I}}^{i}}. Когда говорят о раздутии в замкнутой подсхеме, имеют в виду раздутие в пучке идеалов, который определяет эту подсхему. Подсхема, в которой происходит раздутие, называется центром раздутия. Подмногообразие, появляющееся после раздутия, всегда будет дивизором, называемым исключительным дивизором.

Это определение позволяет раздувать в любой замкнутой подсхеме. Если схема была гладким многообразием, а центр раздутия — её гладким подмногообразием, то, что происходит топологически, можно описать как вырезание малой окрестности центра раздутия и вклеивание проективизации его нормального расслоения, которое на каждом слое выглядит как обобщённое расслоение Хопфа. При раздутии в гладком центре в коразмерности один ничего не происходит. Если же центр не был гладким подмногообразием, то многообразие, вообще говоря, поменяется. Примером могут служить раздутия негладких кривых в особых точках, описанные выше геометрически. Раздутие схемы X{\displaystyle X} во всей схеме X{\displaystyle X} является пустой схемой. В этом случае проблема с терминологией, артикулированная Бондалом, стоит особенно остро: «отображение» раздутия не определено даже локально, а отображение сдутия является тавтологическим включением пустой подсхемы.

Раздутия с центрами в подмногообразиях широко используются в алгебраической геометрии. Так, В. А. Исковских использовал раздутия при классификации трёхмерных многообразий Фано индекса 1 с группой Пикара, изоморфной Z{\displaystyle \mathbb {Z} }.^[7] Непроективное многообразие Хиронаки (англ.)русск. получается последовательными раздутиями точек и кривых в трёхмерном проективном многообразии и последующим склеиванием.

Раздутия иногда являются предметом математических шуток, в первую очередь из-за своего неформального названия. В англоязычной традиции раздутия называются англ. blow-up, что также может быть переведено как «взрыв» (это слово используется в математическом английском и в других контекстах — например, для описания решений дифференциальных уравнений, уходящих на бесконечность за конечное время). Таким образом, выражение «раздуть плоскость в восьми точках» (англ. blow up eight points on a plane) может быть также переведено как «взорвать восемь точек в самолёте». Эта неоднозначность является предметом популярной в математическом сообществе городской легенды об алгебраический геометрах, задержанных в аэропорту за обсуждением раздутий.^[8]

В русскоязычной математической культуре иногда обыгрывается сходство слов англ. blow-up и англ. blowjob.^[9]

1. ↑ Ю. С. Ильяшенко, С. Ю. Яковенко. Аналитическая теория дифференциальных уравнений, ISBN 978-5-4439-0230-2
2. ↑ Д. Б. Каледин. Введение в алгебраическую геометрию, лекция 8
3. ↑ А. Л. Городенцев. Учебные материалы к моему курсу Алгебра — 2 (НМУ, 2014/15 учебный год, 2-й курс)
4. ↑ А. Н. Тюрин. Сборник избранных трудов: В 3-х т. Том 3. Алгебраическая геометрия в топологии и физике. ISBN 5939725880
5. ↑ Ю. И. Манин. Кубические формы: алгебра, геометрия, арифметика. ISBN 978-5-458-44779-9
6. ↑ S. Cantat, S. Lamy. Normal subgroups in the Cremona group (long version), Acta Mathematica 210, p. 31-94, 2013
7. ↑ В. А. Исковских. Двойная проекция из прямой на трёхмерных многообразиях Фано первого рода, Матем. сб., 1989, том 180, номер 2, страницы 260—278
8. ↑ Mathematical «urban legends», MathOverflow
9. ↑ Подслушано вне матфака | IUM, неофициальная страница НМУ в сети ВКонтакте

От вспучивания и раздутия живота. Причины постоянного вздутия живота и методы избавления от проблемы

Показатель	Норма	Отклонения, которые могут быть обнаружены
Форма	Оформленный	Жидкий или кашицеобразный стул возникает при дисбактериозе, кишечных инфекциях, отравлениях, воспалительных заболеваниях кишечника, колитах, болезни Крона, опухолях толстой кишки, пищевой аллергии.
Цвет	Желто-коричневый	Беловатый цвет свидетельствует о патологии печени: гепатите, желчекаменной болезни . Черный цвет и дегтеобразная консистенция могут быть признаком кровотечения из язвы желудка или 12 перстной кишки.
Запах	Каловый нерезкий	Резкий гнилостный запах указывает на недостаток пищеварительных ферментов и резкое увеличение числа гнилостных бактерий.
Реакция	Нейтральная	Щелочная реакция — результат гниения белков в тонкой кишке при дефиците ферментов поджелудочной железы. Кислая реакция — результат брожения углеводов в толстой кишке при углеводной диете.
Мышечные волокна непереваримые	Не обнаружены	Непереваренные элементы мясной пищи присутствуют в кале при снижении кислотности желудочного сока, хроническом панкреатите.
Соединительная ткань	Не обнаружена	Наличие частиц соединительной ткани из пищи возможно при хроническом атрофическом гастрите и воспалении поджелудочной железы (панкреатите), которые сопровождаются дефицитом пищеварительных ферментов .
Скрытая кровь	Не обнаружена	Наличие клеток крови может свидетельствовать о кровоточащих деснах, язвенной болезни , полипах желудка или кишечника, опухоли пищеварительного тракта, глистной инвазии, геморрое .
Слизь	Не обнаруживается невооруженным глазом	Повышенное выделение слизи наблюдается при воспалительных заболеваниях толстой кишки (колитах) и синдроме раздраженного кишечника, а также сальмонеллезе и дизентерии .
Непереваримая клетчатка	В умеренном количестве	Клетчатка в большом количестве говорит о снижении кислотности желудочного сока и заболеваниях поджелудочной железы, если они сопровождаются диареей.
Нейтральный жир	Не обнаружен	Наличие жира вызвано недостатком липазы, выделяемой поджелудочной железой. Встречается преимущественно у больных с хроническим панкреатитом.
Жирные кислоты	Не обнаружены	Наличие жира говорит о патологии поджелудочной железы.
Крахмальные зерна внеклеточные	Не обнаружены	Наличие крахмала в кале может говорить о нарушении всасывания в тонком кишечнике и панкреатите.
Лейкоциты	Не обнаружены или 0-2 в поле зрения	Значительное количество лейкоцитов, отвечающих за борьбу с инфекцией, характерно для воспалительных заболеваний кишечника: колита, кишечных инфекций.
Яйца гельминтов (глистов)	Не обнаружены	Наличие яиц или личинок глистов свидетельствует о заражении гельминтами.
Дрожжевой грибок	Менее 10 3	Увеличение грибка подтверждает дисбактериоз.
Йодофильные бактерии (кокки, палочки)	Не обнаружены	Высокий уровень бактерий указывает на ухудшение пищеварения в желудке, недостаточность ферментов поджелудочной железы и усиленные процессы брожения.
Простейшие (амебы, балантидии, лямблии)	Не обнаружены	Наличие простейших указывает на снижение местного иммунитета (при отсутствие симптомов) или заражение кишечными зоопротонозами (лямблиоз, лейшманиоз).
Стеркобилин и стеркобилиноген	75-350мг/сут	Отсутствует при закупорке желчевыводящих путей. Меньше нормы при паренхиматозных гепатитах, холангитах, дисбактериозе . Превышение нормы возможно при гемолитических анемиях .
Билирубин	Не обнаружен у детей старше года и взрослых	Обнаруживается при дис

5 самых действенных способов избавиться от вздутия живота

Попробуйте интервальное голодание

Недавние исследования показали, что интервальное голодание — один из самых популярных способов похудения и поддержания себя в форме. Многие из пробовавших такое питание утверждают, что оно позволяет уменьшить вздутие менее чем за неделю. Главное правило — потреблять пищу только на протяжении 8 часов в день, а остальные 16 часов давать пищеварительной системе отдохнуть.

Добавляйте имбирь в напитки

Это растение признано одним из самых эффективных противовоспалительных средств. Наиболее сильное действие способен оказывать непосредственно сам корень имбиря, но эффективен также и имбирный чай. Снимая дискомфорт и защищая стенки желудка, имбирь помогает при вздутии, тошноте и боли в животе. Чтобы совместить вкус и пользу, достаточно очистить небольшой кусочек имбиря и добавить его в привычный утренний смузи или просто в воду.

Чаще употребляйте укроп

Еще в древности укроп был известен как средство, способное творить чудеса с пищеварительной системой. В традиционной медицине укроп использовался для устранения боли и предотвращения вздутия. Но и сейчас это природное средство не теряет своей актуальности: недавние исследования показывают, что листья и семена растения обладают противовоспалительными свойствами, а также способны бороться с вирусами и грибками. Семена укропа имеют горьковатый лакричный вкус и могут добавляться в салаты, супы и вторые блюда.

Выбирайте жидкую пищу

Еще один верный способ уменьшить вздутие — это употреблять как можно больше жидкой пищи. Чем мягче еда, тем быстрее она переваривается, потому стоит задуматься над тем, чтобы добавлять больше воды при готовке (в частности, круп) и не спешить убирать пищу с печки. Есть больше супов. Независимо от того, страдаете ли вы от вздутия, это поможет вашему организму лучше переваривать пищу и усваивать больше полезных макро- и микроэлементов.

Контролируйте уровень стресса

Доказано, что вздутие — это не всегда результат неудачного рациона. Например, причиной возникновения этой проблемы может послужить кортизол, также известный как гормон стресса. Исследования показали, что стресс напрямую влияет на пищеварительную систему. Чтобы снизить уровень кортизола, попробуйте лучше высыпаться и уделять время йоге и медитации. Также один из лучших способов борьбы со стрессом — это ходьба. Начинать следует с небольших 20-минутных прогулок.

5 проверенных способов избавиться от вздутия живота

Вы исправно посещаете фитнес и держитесь подальше от холодильника, но ваш живот все равно выглядит, будто вы на пятом месяце беременности?

Скорее всего, причина в плохом составе вашей еды и недостатке физических упражнений. Но есть и менее распространенные причины, например, бактерии в кишечнике или большое количество воздуха, которое вы заглатываете вместе с едой.

Между тем, вздутие живота не такое уж редкое явление. Почти треть взрослого населения страдает от метеоризма, и постоянно задается вопросом, как этого избежать? Есть несколько способов.

Не ешьте большими порциями

Главное правило – ешьте маленькими порциями. То есть вместо огромного ланча, состоящего из первого-второго-третьего-плюс десерт, разделите все это на несколько небольших порций.

При этом важно, чтобы вы правильно жевали. Потому что большие куски увеличивают количество воздуха, которое вы заглатываете с пищей. И как результат – получаете вздутие живота. Ешьте медленно. Жуйте в два раза дольше, чем обычно. И не забывайте пить много воды каждый день.

Проверьте свою пищевую непереносимость

Достаточно часто «добыча газа» в животе усиливается после употребления проблемных продуктов. К самым распространенным пищевым аллергенам в данном случае относятся лактоза, фруктоза, яичные продукты и глютен. Какой продукт не гуд именно для вас?

Попробуйте такой эксперимент — на пару недель исключите из своего рациона вышеуказанные продукты (предпочтительно по одному), и если вы заметите изменения, просто откажитесь от них.

Прекратите, наконец, пить газировку

Одним из самых больших источников вздутия становятся газированные напитки и шипучки. Именно содержащиеся в них пузырьки — причина того, что вы так и не можете получить плоский живот. Прекратите пить их раз и навсегда, и забудете о своем недуге!

Кстати, жевательная резинка, употребление алкоголя и напитки через соломинку тоже провоцируют чрезмерное количество газов.

Излечитесь от синдрома раздраженного кишечника

Синдром раздраженного кишечника является относительно распространенным заболеванием, которое затрагивает приблизительно четырнадцать процентов людей. Однако большая часть людей даже не подозревает о том, что имеет данную проблему.

Между тем, наиболее распространенные симптомы синдрома раздраженного кишечника — это вздутие живота, боли в животе, диарея или, наоборот, запор. Если эти симптомы вам знакомы, обратитесь к врачу.

Поосторожней с алкоголем!

Содержание сахара в спирте часто вызывает проблемы с пищеварением, потому что это способствует размножению бактерий в кишечнике, что, в свою очередь, приводит к избыточному содержанию газов. Ограничьте потребление алкоголя, а если вы решите пить, выбирайте менее сладкие напитки, например, сухие вина.

Избегайте ликеры, коктейли и алкогольные напитки в баночках.

КСТАТИ

— Нарушение микрофлоры кишечника может быть вызвано плохоперевариваемыми продуктами, это бобовые, орехи, фрукты, ячмень, брюссельская капуста, семечки, овес, мед и дрожжи, — говорит профессор Ашот Хачатрян, Академик Российской академии медико-технических наук. – В домашних условиях от вздутия живота можно избавиться с помощью кисломолочных продуктов, таких как йогурт, кефир. Если вздутие живота становится постоянной проблемой, это говорит о том, что у вас может быть непроходимость кишечника, закупорка мочевыводящих путей, а то вовсе аппендицит. В этом случае с визитом к врачу тянуть не рекомендуется.

ЧИТАЙТЕ ТАКЖЕ

Можно ли стать стройной, обвязав талию ниткой?

Человеческий гений не стоит на месте, и теперь живот можно сделать плоским без занятий в спортзале и бега трусцой. Для этого по утрам, надев трусы и часы, надо обвязать свою талию ниткой. Она не позволит расслабить мышцы пресса, которые всегда будут в тонусе, и вскоре талия волшебно уменьшится на несколько сантиметров! Ну во всяком случае так обещают (дальше)

Не жалея живота своего: Ляйсан Утяшева поможет вам сделать талию к лету

Обнаружился животик, который предательски выглядывает из джинсов и портит весь внешний вид? Ляйсан Утяшева напоминает, что быстрая сгонка веса только вредит организму, а мышцы за один день, к сожалению, не подкачиваются. Начнем лепить фигуру с талии и животика (дальше)

Причины и лечение метеоризма и газообразования

Любые неприятные ощущения в желудке доставляют дискомфорт. Усиливающаяся боль или образование газов могут не только испортить настроение, но и стать причиной отмены встречи или поездки. Не обязательно бежать за лекарством. Чтобы избавиться от вздутия живота, используйте простые и доступные способы.

Пейте больше воды

Если вы имеете предрасположенность к метеоризму, не употребляйте газированные напитки. Содержащиеся в них пузырьки скапливаются в животе, вызывают вздутие, и появляется боль. Пейте простую очищенную воду. Она выводит из организма токсины, шлаки, помогает переваривать пищу, ускоряет доставку полезных веществ.

Достаточное количество выпитой за день воды избавляет от запоров.

Ешьте маленькими кусочками

Одна из главных причин, вызывающих повышенное газообразование – глотание воздуха при употреблении пищи. Чтобы этого избежать, старайтесь не разговаривать во время еды, не пейте через коктейльные соломки, избегайте перекусов. Не хватайте еду большими кусками и жуйте ее, не открывая рот. Меньше употребляйте продуктов, которые вызывают газообразование (фасоль, горох, капуста, виноград).

Ешьте больше клетчатки

Она работает, как щетка, и очищает кишечник, избавляет от запоров, улучшает пищеварение. Клетчатка восстанавливает микрофлору, помогает бороться с изжогой. Дневная норма употребления для мужчин – 33,5 г, а для женщин – 28 г.

Чтобы восполнить недостаток клетчатки, начинайте утро с полезного завтрака, добавляйте отруби. Набухая в кишечнике, они помогают остаткам пищи быстрее двигаться.

Днем перекусывайте свежими овощами, фруктами. Особенно полезны апельсины, арбуз, т. к. на 90% состоят из воды и содержат необходимые волокна.

Изменяйте рацион постепенно, иначе живот будет бурлить, вздуваться. Организму нужно время, чтобы привыкнуть к обработке дополнительной клетчатки.

Больше двигайтесь

Простая 10-минутная прогулка быстрым шагом поможет избавиться от любого вздутия живота. Людям, предрасположенным к метеоризму, полезны упражнения на брюшной пресс. Физические нагрузки – лучшее средство от вздутия живота. Они помогают газам быстрее проходить через пищеварительный тракт.

Будьте осторожны с молочными продуктами

Обратите внимание, после какой еды в животе наступает дискомфорт. Попробуйте убрать из рациона молочные продукты, содержащие лактозу. Приобретенная непереносимость этого вещества часто встречается у пожилых людей.

Выбирайте кисломолочные продукты с низким процентом жирности.

Пейте кефир, ряженку, йогурты – они более безопасны, чем молоко. Кушайте творог, сыр, но не злоупотребляйте их количеством. Если живот надувается, тяжесть не проходит, принимайте фермент Лактаза. Препарат улучшает усвоение молочных продуктов и пищеварение.

Проверьте свою аптечку

Убрать газы в кишечнике поможет мята перечная. Ее выпускают в виде таблеток и капсул. Эффективно снимает вздутие активированный уголь. Эти средства сделаны из натуральных ингредиентов, поэтому не приносят вред организму. Они расслабляют пищеварительные мышцы, поглощают газ.

Вздутие и запоры могут вызывать антидепрессанты, препараты от аллергии, железосодержащие таблетки и некоторые другие лекарства.

Их побочные действия особенно выражены в первые дни. Если после приема таблеток появился дискомфорт в животе, вздутие или диарея, проконсультируйтесь у терапевта или гастроэнтеролога.

Видео

2847

Была ли эта статья полезной?

Да

Нет

24 человек ответили

Спасибо, за Ваш отзыв!

человек ответили

Что-то пошло не так и Ваш голос не был учтен.

Нашли в тексте ошибку?

Выделите её, нажмите Ctrl + Enter и мы всё исправим!

вспучивание — это… Что такое вспучивание?

вспучивание — набухание, взбухание, пучина, вздутие, пученье Словарь русских синонимов. вспучивание сущ. • вздувание • взбухание • набухание • раздувание Словарь русских синонимов. Контекст 5.0 Информатик. 2012 …   Словарь синонимов

вспучивание — Увеличение объёма пластичного материала с образованием ячеистой структуры в результате выделения газа или пара в объёме этого материала [Терминологический словарь по строительству на 12 языках (ВНИИИС Госстроя СССР)] Тематики строительные изделия …   Справочник технического переводчика

Вспучивание — – аномальное увеличение объема уложенной и уплотнен­ной бетонной смеси в результате выделения газа вслед­ствие химических процессов в гидратирующемся це­менте или расширения вовлеченного воздуха при на­гревании. [Терминологический словарь… …   Энциклопедия терминов, определений и пояснений строительных материалов

вспучивание — išsipūtimas statusas T sritis radioelektronika atitikmenys: angl. blister; buckling vok. Aufbauchung, f; Aufblähung, f rus. вздутие, n; вспучивание, n pranc. formation de bulles, f; gonflage, m; gonflement, m …   Radioelektronikos terminų žodynas

Вспучивание — ср. 1. процесс действия по гл. вспучивать I, вспучиваться 1. 2. Результат такого действия. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 …   Современный толковый словарь русского языка Ефремовой

ВСПУЧИВАНИЕ — увеличение объёма пластичного материала с образованием ячеистой структуры в результате выделения газа или пара в объёме этого материала (Болгарский язык; Български) набъбване; експандиране (Чешский язык; Čeština) nadouvání; expandování (Немецкий… …   Строительный словарь

вспучивание — всп учивание, я …   Русский орфографический словарь

вспучивание — (2 с), Пр. о вспу/чивании …   Орфографический словарь русского языка

Вспучивание — [swelling; bulging] увеличение в объеме твёрдых шихтовых материалов, обусловленных выделением газов …   Энциклопедический словарь по металлургии

вспучивание — я; ср. к Вспучить вспучивать и Вспучиться вспучиваться. В. живота …   Энциклопедический словарь

вспучивание — я; ср. к вспучить вспучивать и вспучиться вспучиваться. Вспу/чивание живота …   Словарь многих выражений